《线性代数》财大成教原题及答案 图1

1、设A和B为n阶方阵,下列运算正确的是( )
A、|-A|=|A|
B、|AB|=|A||B|
C、(A-B)(A+B)=A²-B²
D、A²=A⇒A=o或A=1
答案:B
2、设A=
《线性代数》财大成教原题及答案 图2
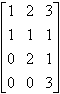 则r(A)=( )
则r(A)=( )
A、1
B、2
C、3
D、4
答案:C
3、n阶矩阵A是正定矩阵的充要条件是( )
A、|A|>0
B、矩阵A的负惯性指标为 0
C、矩阵A是可逆矩阵
D、矩阵A的正惯性指标是n
答案:D
4、设非齐次线性方程组AX=B的任意两个解为”n₁,n₂”,其导出组为 AX=0,则下列结论错误的是( )
A、n₁-n₂是AX=0的一个解
B、(1/2)n₁ + (1/2)n₂是AX=B的一个解
C、n₁+n₂"是AX=0的一个解
D、2n₁ - n₂是AX=B的一个解
答案:C
5、排列n(n-1)…1的逆序数是( )
A、n
B、n-1
C、[n(n-1)]/2
D、n(n+1)/2
答案:C
6、设A为3阶方阵,B为4阶方阵,且1A|=1,|8|=-2,则行列式||B|A|之值为( )
A、-8
B、-2
C、2
D、8
答案:A
7、设A、B为n阶可逆阵,则下列等式成立的是( )
《线性代数》财大成教原题及答案 图3
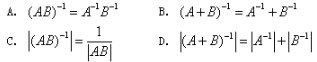
答案:C
8、设A=[a₁,a₂,a₃],其中 a₁(i=1,2,3)是三维列向量,若|A|=1,则 |[4a₁,2a₁-3a₂,a₃]|( )
A、-24
B、-12
C、12
D、24
答案:B
9、设 A、B 为同阶方阵,下列等式中恒正确的是( )
A、AB=BA
B、(A+ B)⁻¹= A⁻¹+ B⁻¹
C、|A+B|=|A|+|B|
D、(A+B)ʳ=Aʳ +Bʳ
答案:D
1、设3阶矩阵A=
《线性代数》财大成教原题及答案 图4
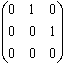 ,则A²的秩为()、
,则A²的秩为()、
A、0
B、1
C、2
D、3
答案:B
2、设向量组I能由向量组II线性表示,则有( )
A、r(I)<r(II)
B、r(I)≤r(II)
C、r(I)≥r(II)
D、r(I)>r(II)
答案:B
3、设A是m×n的矩阵,已知齐次线性方程组AX=0有非零解,且r(A)=r,则其基础解系所含解向量的个数为( )
A、n
B、n-r
C、r
D、n-r+1
答案:B
4、设A,B是n阶矩阵,若A-B,则下列命题不正确的是( )
A、若A可逆,则B可逆
B、A和B是等价的
C、A知B具有相同的迹
D、A和B是合同的
答案:D
5、以A为系数矩阵的齐次线性方程组有非零解的充要条件是( ).
A、系数矩阵A的任意两个列向量线性相关
B、系数矩阵A的任意两个列向量线性不相关
C、必有一列向量是其余列向量的线性组合
D、任一列向量都是其余列向量的线性组合
答案:C
6、
《线性代数》财大成教原题及答案 图5
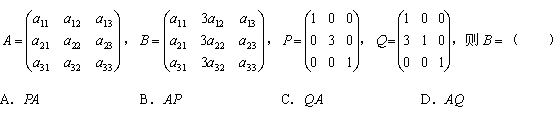
答案:B
7、已知A为n阶方阵,且|A|≠0,则下列命题不正确的是( )
A、A的列向量组是线性无关的
B、A的所有特征值都不为0
C、矩阵A的秩为n
D、线性方程组AX=B有无穷多解
答案:D
8、设3阶方阵 A的行列式为2,则|-(1/2)A|=()
A、-1
B、-(1/4)
C、1/4
D、1
答案:B
9、已知α,β,δ线性无关,α,β,δ线性相关,则( )
A、α必可由α,β,δ线性表出
B、β必不可由α,β,δ线性表出
C、δ必可由α,β,δ线性表出
D、δ必不可由α,β,δ线性表出
答案:C
10、设A,B,C均为n阶方阵,AB=BA,AC=CA,则ABC=( )
A、ACB
B、CAB
C、CBA
D、BCA
答案:D
11、向量组
《线性代数》财大成教原题及答案 图6
 线性无关的充要条件是( )
线性无关的充要条件是( )
《线性代数》财大成教原题及答案 图7

答案:D
12、
《线性代数》财大成教原题及答案 图8
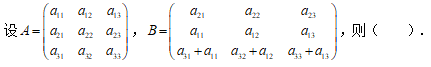
A、r(A)=r(B)
B、r(A)<r(B)
C、r(A)>r(B)
D、不能确定
答案:A
1、设 A,B是任意的 n阶方阵,下列命题中正确的是( )
A、(A+B)²=A²+2AB+B²
B、(A+B)(A-B)=A²-B²
C、(A-E)(A+E)=(A+E)(A-E)
D 、(AB)²= A²B²
答案:C
2、设A、B均为方阵,则下列结论中正确的是( )
A、若|AB|=0,则A=0或B=0
B、若|AB|=0,则|A|=0或|B|=0
C、若AB=0,则A=0或B=0
D、若AB≠0,则|A|≠0或|B|≠0
答案:B
3、设
《线性代数》财大成教原题及答案 图9
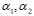 是矩阵A的属于特征值λ的特征向量,则下列结论一定成立的是( )
是矩阵A的属于特征值λ的特征向量,则下列结论一定成立的是( )
A、a₁+a₂是A的属于特征值λ的特征向量
B、2a₁是A的属于特征值λ的特征向量
C、对于任意给定的实数k₁,k₂,k₁a₁+k₂a₂是A属于特征值λ的特征向量
D、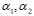 一定线性无关 一定线性无关
答案:B
4、若矩阵A的秩为r,则下列命题正确的是( )
A、所有的r-1阶子式都不等于0
B、所有的r-1阶子式全等于0
C、至少有一个r阶子式不等于0
D、所有的r阶子式都不等于0
答案:C
5、设A为三阶方阵且|A=-2则I3AʳA|=( )
A、-108
B、 -12
C、12
D、108
答案:D
6、设A为三阶矩阵,且|A⁻¹|=3,则|-3A|=( )
A、-9
B、 -1
C、1
D、9
答案:A
7、设A=
《线性代数》财大成教原题及答案 图10
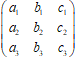 ,若AP=
,若AP=
《线性代数》财大成教原题及答案 图11
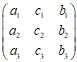 ,则P=( )
,则P=( )
《线性代数》财大成教原题及答案 图12
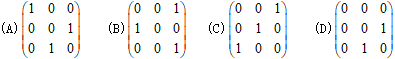
答案:A
8、设4是4阶方阵,且|A|≠0,则|A*|=( )
A、|A|
B、|A|²
C、|A|³
D、|A|⁴
答案:C
1、已知 A是一个3x4矩阵,下列命题中正确的是( )
A、若矩阵 A中所有 3阶子式都为 0,则秩(A)=2
B、若A中存在 2阶子式不为0,则秩(A)=2
C、若秩(A)=2,则A中所有 3阶子式都为0
D、若秩(A)=2,则A中所有 2阶子式都不为 0
答案:C
2、设A,B是n阶矩阵,若P,Q为n阶可逆矩阵且A=PBQ,则下列命题不正确的是( )
A、若4可逆,则B可逆
B、A和B是等价的
C、A和B具有相同的迹
D、r(A)=r(B)
答案:C
3、设矩阵A=
《线性代数》财大成教原题及答案 图13
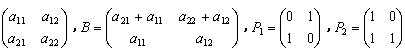 ,则必有()
,则必有()
A、P₁P ₂A=B
B、P ₂P₁A=B
C、AP₁P ₂=B
D、AP ₂P₁=B
答案:A
4、已知三阶行列式
《线性代数》财大成教原题及答案 图14
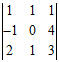 ,则A₃₁+A₃₂+A₃₃=( )
,则A₃₁+A₃₂+A₃₃=( )
A、1
B、0
C、6
D、4
答案:B
1、二次型
《线性代数》财大成教原题及答案 图15
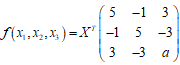 X的秩为2,则a的取值为( )
X的秩为2,则a的取值为( )
A、0
B、1
C、2
D、3
答案:D
2、若
《线性代数》财大成教原题及答案 图16
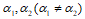 是线性方程组4X=B的两个解向量,
是线性方程组4X=B的两个解向量,
《线性代数》财大成教原题及答案 图17
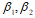 是导出组AX=0的基础解系,则下列说法正确的是( )
是导出组AX=0的基础解系,则下列说法正确的是( )
A、α₁ +α₂+β₁,为线性方程组AX=B的解向量
B、α₁+2α₂-β₂为线性方程组AX=B的解向量
C、线性方程组AX=B的通解为α₁,+α₂+c₁β₁+c₂β₂,,c₁c₂为任意常数
D、线性方程组AX=B的通解为(α₁,+α₂)/2+c₁β₁+c₂β₂, c₁c₂为任意常数
答案:D
3、已知五阶行列式D=|aₛ|,下面哪一个不是该行列式中的项( )
A、a₁₁a₂₂a₃₃a₄₄a₅₅
B、a₁₂a₂₁a₃₄a₄₅a₅₃
C、a₁₂a₂₃a₃₄a₄₄a₅₁
D、a₁₃a₂₅a₃₄a₄₂a₅₁
答案:C
4、当ab≠bc时,矩阵=
《线性代数》财大成教原题及答案 图18
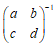 ()
()
《线性代数》财大成教原题及答案 图19

答案:B
5、设A=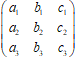 ,若AP= ,若AP=
《线性代数》财大成教原题及答案 图20
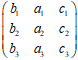 ,则P=( )
,则P=( )
《线性代数》财大成教原题及答案 图21
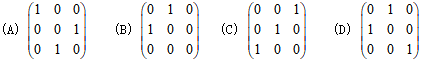
答案:D
|