河南财大成教《概率论与数理统计》专升本课程原题及答案 图1
1、已知随机变量x的概率函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图2
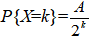,k=1,2,…，则A=( )
A、2
B、1
C、1/2
D、1/3
答案：B
2、设二维随机变量(X,Y）的分布律为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图3
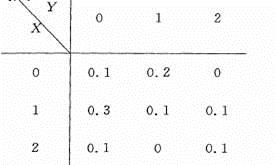
A、0.3
B、0.5
C、0.7
D、0.8
答案：A
3、设随机变量X服从参数λ=1的泊松分布，Y~B(4,0.8).已知 D(X+Y)=2.6，则它们的相关系数
河南财大成教《概率论与数理统计》专升本课程原题及答案 图4
=_____________
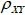A、0.8
B、0.7
C、0.6
D、0.5
答案：C
4、设A，B为两个随机事件，且B⊂A，P(B)>0，则P(A|B)=( ）
A、1
B、P(A)
C、P(B)
D、P(AB)
答案：A
5、设随机变量Y服从参数为1的指数分布，则关于x的二次方程4x²+4xY+Y+2=0 有实根的概率为( )
A、3/5
B、
河南财大成教《概率论与数理统计》专升本课程原题及答案 图5
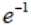
C、
河南财大成教《概率论与数理统计》专升本课程原题及答案 图5
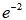
D、e²
答案：C
6、已知P(A)=0.6，P(A-B)=0.3，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图6
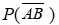为( )
A、0.6
B、0.7
C、0.8
D、0.9
答案：B
7、已知事件A，B，A∪B的概率分别为0.5,0.4,0.6，则P(A
河南财大成教《概率论与数理统计》专升本课程原题及答案 图7
)
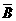A、0.1
B、0.2
C、0.3
D、0.5
答案：B
8、有三枚硬币，其中一枚两面都是正面图像，另一枚两面都是反面图像，第三枚是正常硬币.现从中任取一枚进行抛掷，得到正面向上，则另一面是反面的概率为____________
A、1/4
B、1/3
C、1/2
D、1/5
答案：B
9、设A，B为两个随机事件，且B⊂A，P(B)>0，则P(A|B)=（ ）
A、1
B、P(A)
C、P(B)
D、P(AB)
答案：A
10、设二维随机向量（X,Y）只取四个点(0,0),(1,1),(1,2),(2.0)，且相应概率依次为1/2,1/6,1/6,a,则P(Y=0)=( )
A、7/12
B、1/2
C、1/6
D、2/3
答案：D
11、设A与B是任意两个互不相容事件，则下列结论中正确的是（ ）
A、P(A)=1-P(B)
B、P(A-B)=P(B)
C、P(AB)=P(A)P(B)
D、P(A-B)=P(A)
答案：D
12、已知Y=-3X+1，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图8
=（ ）
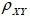A、0
B、1
C、-1
D、2
答案：C
13、设 A、B 为任意两个事件，则有( ）
A、（A∪B）- B = A
B、（A-B）∪B = A
C、（A∪B）- B ⊂ A
D、（A-B）∪B ⊂ A
答案：C
14、设(X,Y)服从区域 D={(x,y)|0<x<1,0<y<1}上的均匀分布，则P{X+Y≤1}= ( )
A、π/2
B、1/2
C、π/4
D、1/4
答案：B
15、已知随机变量X的概率函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图9
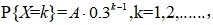则A=（）
A、0.7
B、0.6
C、0.5
D、0.4
答案：A
16、抛掷两枚硬币，若事件A表示“至少一枚为正面”，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图10
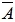表示（ ）
A、至少一枚为反面
B、至少一枚不为反面
C、两枚皆为反面
D、两枚皆为正面
答案：C
17、设随机变量x的概率密度为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图11
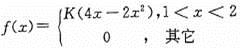则K=（ ）。
A、5/16
B、1/2
C、3/4
D、4/5
答案：C
18、设随机变量X～B(3，0.4)，则P{X≥1}=( )
A、0.352
B、0.432
C、0.784
D、0.936
答案：C
19、将一枚均匀的硬币抛掷三次，恰有一次出现正面的概率为（ ）
A、0.125
B、0.25
C、0.375
D、0.5
答案：C
20、设(X,Y)~N(1,1,1,1,0.5)，则Cov(2x,Y+3)=( )
A、5
B、3
C、1
D、4
答案：C
21、有10个零件,其中混入了2个次品,从中随机地抽取3个,其中最多一个正品的概率为（）
A、2/10
B、1/10
C、8/15
D、7/15
答案：C
22、设（X,Y）的联合概率密度为f(x,y)=
河南财大成教《概率论与数理统计》专升本课程原题及答案 图12
,则P{Y≤X}=（ ）
A、0.1
B、0.2
C、0.3
D、0.4
答案：D
23、某人射击三次，其命中率为0.7，则三次中至多击中一次的概率为( ）
A、0.027
B、0.081
C、0.189
D、0.216
答案：D
24、二维随机变量（x,Y）的联合概率密度为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图13
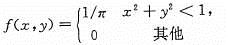
则随机变量x与y为（ ）。
A、独立同分布
B、独立不同分布
C、不独立同分布
D、不独立不同分布
答案：A
25、设随机变量X的取值为0,1,2,3，取这些值的概率分别为0.2,0.3，k,0.1,则k=（ ）
A、0.1
B、0.2
C、0.3
D、0.4
答案：D
26、随机变量x的密度函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图14
，则常数 A=( ）
A.1
B.1/2
C.1/3
D.1/4
答案：B
27、投掷两枚骰子，事件A表示第一次得到“1”点，下列事件与事件A不独立的是（）
A、第二次得到“1”点；
B、第二次得到“3”点；
C、两次点数之和为7；
D、两次点数之和为8；
答案：D
28、己知随机变量x~N(2,9)，则下列随机变量服从 N(0,1)的是（ ）
A、(X+2)/3
B、(X-2)/3
C、(X+2)/9
D、(X-2)/9
答案：B
29、随机变量X的分布函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图15
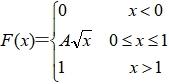，则P{-1≤x≤0.25}=( )
A、1
B、1/4
C、1/2
D、1/3
答案：C
30、设A，B为两事件，已知P(A)=1/3，P(A|B)=，P(BIA)=2/3，P(
河南财大成教《概率论与数理统计》专升本课程原题及答案 图16
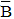|A)=3/5，则P(B)=( )
A、1/5
B、2/5
C、3/5
D、4/5
答案：A
31、设随机变量X，Y相互独立，且X~N（2，1），Y~N（1，1），则（ ）
A.P{X-Y≤1}=0.5
B. P{X-Y≤0}=0.5
C. P{X+Y≤1}=0.5
D. P{X+Y≤0}=0.5
答案：A
32、下列说法正确的是：（）
A.若事件A、B互不相容，则事件A、B独立；
B.若事件A、B独立，则事件A、B互不相容；
C.若事件A是必然事件，则P(A)=1；
D.若P(A)=1，则事件A是必然事件
答案：C
33、抛掷两枚硬币，若事件A表示“两枚皆为反面”，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图17
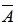表示
A、至少一枚为正面
B、至少一枚为反面
C、两枚皆为正面
D、两枚皆不为正面
答案：A
34、X服从区间[-1,1]上的均匀分布，服从参数为2的指数分布，且x与Y独立，则D(X-2Y+1)=( )
A、1/3
B、5/6
C、4/3
D、7/3
答案：C
35、某人射击三次，其命中率为0.8，则三次中至多命中一次的概率为（ ）。
A、0.002
B、0.04
C、0.08
D、0.104
答案：D
36、设事件 A，B互不相容，已知P(A)=0.4，P(B)=0.5，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图18
=（ ）
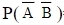A、0.1
B、0.4
C、0.9
D、1
答案：A
37、设随机变量 X，Y相互独立，x~N(0,2²),Y 服从区间[1,3]的均匀分布，则D(X-3Y)=( )
A、7
B、1
C、5
D、3
答案：A
38、己知随机变量X的概率函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图19
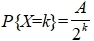,k=1,2,…，则A=( )
A、0
B、1/4
C、1/2
D、1
答案：D
39、根据以往的资料，某一三口之家患某种传染病的概率有以下规律： P{孩子得病}=0.6，P{母亲得病|孩子得病}=0.5，P{父亲得病|母亲及孩子得病}=0.4，则母亲及孩子得病而父亲未得病的概率为（）
A、0.18
B、0.12
C、0.08
D、0.16
答案：A
40、设随机变量X的分布函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图20
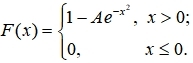则A=( )
A、0
B、1/2
C、1
D、2
答案：C
41、设随机变量X和Y有DX=25，DY=36，
河南财大成教《概率论与数理统计》专升本课程原题及答案 图21
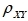=0.4，则 D(X+Y)=( )
A、37
B、49
C、73
D、85
答案：D
42、投掷两枚骰子，事件A表示第一次得到“5”点，下列事件与事件A独立的是（）
A、两次点数之和为5
B、两次点数之和为6；
C、两次点数之和为7；
D、两次点数之和为8；
答案：C
43、随机变量X的取值为-1,0,1，概率比为1：2：3，则EX=（）
A、1/3
B、1/2
C、2/3
D、1/6
答案：A
44、已知随机变量X~N(3,4)，则下列随机变量服从 N(0,1)的是( )
A、(X-3)/2
B、(X+3)/2
C、(X-3)/4
D、(X+3)/4
答案：A
45、设书籍中每页的印刷错误数服从泊松分布，经统计发现在某本书上，有一个印刷错误的页数与有2个印刷错误的页数相同，任意检验4页，恰有2页上没有印刷错误的概率为( )
河南财大成教《概率论与数理统计》专升本课程原题及答案 图22
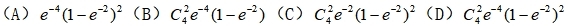
答案：D
46、同时抛掷3枚均匀的硬币，则恰好三枚均为正面朝上的概率为( )
A、0.125
C、0.375
B、0.25
D、0.5
答案：A
47、设随机事件A与B互不相容，P(A)=0.2，P(B)=0.4，则P(B|A)=( )
A、0
B、0.2
C、0.4
D、1
答案：A
48、假设X服从区间[0,1]上的均匀分布，Y服从参数为1的指数分布，并且彼此相互独立，则P(Y≤X)=( )
河南财大成教《概率论与数理统计》专升本课程原题及答案 图23
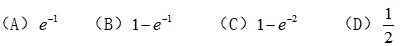
答案：A
阶段测验
1、设二维随机向量(X,Y)只取四个点(0,0)，(-1,1)，(1,-1)，(1,1)，且相应的概率依次为2/3,1/6,1/9,1/18，则F(0,1)=( ) A、1/6 B、2/3 C、5/6 D、1 答案：C
2、有三枚硬币，其中一枚两面都是正面图像，另一枚两面都是反面图像，第三枚是正常硬币.现从中任取一枚进行抛掷，得到正面向上，则另一面是反面的概率为____________ A、1/4 B、1/3 C、1/2 D、1/5 答案：B
3、假设X服从区间[0,1]上的均匀分布，Y服从参数为1的指数分布，并且彼此相互独立，则P(Y≤X)=( )
河南财大成教《概率论与数理统计》专升本课程原题及答案 图24
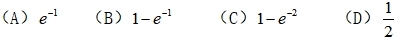
答案：A
4、设随机变量X，Y相互独立，X~N(0,2²),Y服从区间[1,3]的均匀分布，则D(X-3Y)=( ) A、7 B、1 C、5 D、3 答案：A
5、随机变量X的取值为-1,0,1，概率比为1：2：3，则EX=（） A、1/3 B、1/2 C、2/3 D、1/6 答案：A
6、假设X和都服从区间[0,1]上的均匀分布，并且彼此相互独立，则P{Y≤X²}=( ） A、1/5 B、1/4 C、1/3 D、1/2 答案：C
7、己知随机变量X的概率函数为P{X=k}=A·
河南财大成教《概率论与数理统计》专升本课程原题及答案 图25
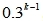
,k=1,2,……，则A=( ） A、0.7 B、0.6 C、0.5 D、0.4 答案：A
8、设随机变量X和Y有DX=25，DY=36，
河南财大成教《概率论与数理统计》专升本课程原题及答案 图26
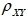
=0.4，则D(X+Y)=（ ） A、37 B、49 C、73 D、85 答案：D
9、根据以往的资料，某一三口之家患某种传染病的概率有以下规律： P{孩子得病}=0.6，P{母亲得病|孩子得病}=0.5，P{父亲得病|母亲及孩子得病}=0.4，则母亲及孩子得病而父亲未得病的概率为（） A、0.18 B、0.12 C、0.08 D、0.16 答案：A 10、已知随机变量X的概率函数为P{X=k}=
河南财大成教《概率论与数理统计》专升本课程原题及答案 图27
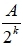
,k=1,2,…，则A=( ) A、0 B、1/4 C、1/2 D、1 答案：D 11、设(X,Y)的联合概率密度为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图28
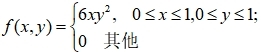
，则P{Y≤X}=( ) A、0.1 B、0.2 C、0.3 D、0.4 答案：D
12、下列说法正确的是：（） A、若事件A、B互不相容，则事件A、B独立； B、若事件A、B独立，则事件A、B互不相容； C、若事件A是必然事件，则P(A)=1； D、若P(A)=1，则事件A是必然事件. 答案：C
13、已知随机变量X~N(2,9)，则下列随机变量服从 N(0,1)的是( ) A、(X+2)/3 B、(X－2)/3 C、(X+2)/9 D、(X－2)/9 答案：B 14、已知随机变量X的概率函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图29
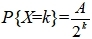
,k=1,2,…，则A=( ) A、2 B、1 C、1/2 D、1/3 答案：B
15、设书籍中每页的印刷错误数服从泊松分布，经统计发现在某本书上，有一个印刷错误的页数与有2个印刷错误的页数相同，任意检验4页，恰有2页上没有印刷错误的概率为( )
河南财大成教《概率论与数理统计》专升本课程原题及答案 图30
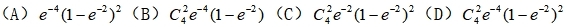
答案：D
16、已知Y=-3X+1,则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图31
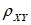
=（ ） A、0 B、1 C、-1 D、2 答案：C
17、有10个零件,其中混入了2个次品,从中随机地抽取3个,其中至少有1个次品的概率为（）. A、1/10 B、2/10 C、7/15 D、8/15 答案：D
18、设(X,Y)~N(1,1,1,1,0.5)，则Cov(2x,Y+3)=( ) A、5 B、3 C、1 D、4 答案：C 19、随机变量X的分布函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图32
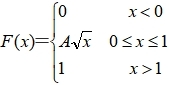
，则P{-1≤X≤0.25}=( ) A、1 B、1/4 C、1/2 D、1/3 答案：C
20、抛掷两枚硬币，若事件A表示“两枚皆为反面”，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图33
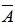
表示（ ） A、至少一枚为正面 B、至少一枚为反面 C、两枚皆为正面 D、两枚皆不为正面 答案：A
21、已知随机变量X~N(3,4)，则下列随机变量服从 N(0,1)的是( ) A、(X-3)/2 B、(X+3)/2 C、(X-3)/4 D、(X+3)/4 答案：A
22、抛掷两枚硬币，若事件A表示“至少一枚为正面”，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图34
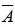
表示( ) A、至少一枚为反面 B、至少一枚不为反面 C、两枚皆为反面 D、两枚皆为正面 答案：C
23、有10个零件,其中混入了2个次品,从中随机地抽取3个,其中最多一个正品的概率为（） A、2/10 B、1/10 C、8/15 D、7/15 答案：C
24、设随机变量X服从参数λ=1的泊松分布，Y~B(4,0.8).已知 D(X+Y)=2.6,则它们的相关系数
河南财大成教《概率论与数理统计》专升本课程原题及答案 图35
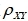
=___________ A、0.8 B、0.7 C、0.6 D、0.5 答案：C
25、已知P(A)=0.6，P(A-B)=0.3，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图36
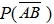
为( ) A、0.6 B、0.7 C、0.8 D、0.9 答案：B
1、抛掷两枚硬币，若事件A表示“两枚皆为反面”，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图37
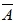
表示“两枚皆为正面”。 A、正确 B、错误 答案：B
2、设随机变量X和Y有DX=25,DY=36,
河南财大成教《概率论与数理统计》专升本课程原题及答案 图38
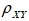
=0.4,则D(X-Y)=37。 A、正确 B、错误 答案：A
3、设X~N(0,1)，则Φ(-x)=Ф(x). A、正确 B、错误 答案：B
4、若E(XY)=E(X)E(Y)，则X与Y相互独立. （ ） A、正确 B、错误 答案：B
5、设(X,Y)~N
河南财大成教《概率论与数理统计》专升本课程原题及答案 图39
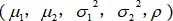
，则X与Y相互独立的充要条件为ρ=0. A、正确 B、错误 答案：A 6、设X~B(n,p),则由中心极限定理可得
河南财大成教《概率论与数理统计》专升本课程原题及答案 图40
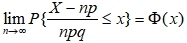
A、正确 B、错误 答案：A
7、设(X,Y)~N(1,1,3²,4²,0.5)，则 Cov(X+4, 4Y)=24.
A、正确 B、错误 答案：A
8、 若在每次试验中，事件A不出现的概率为0.3，则在27次独立重复试验中，A最可能出现的次数为8次.()
A、正确 B、错误 答案：B
9、设随机变量X的分布函数为F(x)，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图41
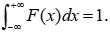
A、正确 B、错误 答案：B
10、若B⊂A，则P(B|A)≥P(B) A、正确 B、错误 答案：A
11、设(X,Y)服从区域 D={(x,y)|0<x<1,0<y<1}上的均匀分布，则P{X+Y≤1}=0.5. A、正确 B、错误 答案：A
12、已知随机变量X~N(2,9)，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图42
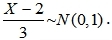
A、正确 B、错误 答案：A
13、对于二维连续型随机向量(X,Y)的联合密度函数f(x,y)和边缘密度函数fx(x),fy(y)，一定有
河南财大成教《概率论与数理统计》专升本课程原题及答案 图43
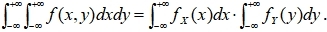
A、正确 B、错误 答案：A
14、 已知P(A)=0.8，P(A-B)=0.4，当A与B独立时，P(B)=0.4.()
A、正确 B、错误 答案：B
15、 连续型随机变量的密度函数一定是连续函数. （ ）
A、正确 B、错误 答案：B
16、 若D(X+Y)=D(X-Y)，则X与Y一定不相关. （ ）
A、正确 B、错误 答案：A
17、 若X与Y不相关，则E(XY)=EXEY.()
A、正确 B、错误 答案：A
18、设(X,Y)服从区域 D 上的均匀分布，其中D={(x,y)|x²+y²≤1}，则(X,Y)的联合密度函数为f(x,y)=1/π。
A、正确 B、错误 答案：B
19、 设X~B(n1,p)，Y~B(n2,p)，且X与Y独立，则X+Y~B(n1+n2,p).()
A、正确 B、错误 答案：A
20、 若A与B相互独立，则A与B互斥. （ ）
A、正确 B、错误 答案：B
二、填空
21、已知随机变量X的概率函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图44
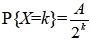
,k=0,1,2,……则A=__________________ 答案：1/2
22、设随机变量X,Y相互独立，X~N(1,4)，Y服从区间[1,3]上的均匀分布，则D(X-3Y)=______________ 答案：7
23、已知Y=-X+1，则
河南财大成教《概率论与数理统计》专升本课程原题及答案 图45
=_______________
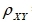
答案：-1 24、随机变量X的分布函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图46
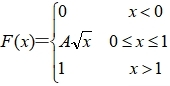
,系数 A=___________ 答案：1
25、设随机变量X与Y相互独立，X~N(1,4)，Y服从区间[1,3]上的均匀分布,则D(X+3y)=__________ 答案：7
26、随机变量X只取-1, 0, 1三个值，且相应概率的比为1: 2: 3,则EX=___________ 答案：1/3
27、二维随机变量(X，y)的联合分布列为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图47
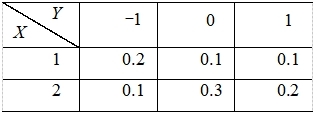
设Z=Y/X，则E(Z)=____________________
28、为了防止意外，在矿内同时设有两种报警系统A与B，每种系统单独使用时有效的概率为：系统A为0.92，系统B为0.93；在A失灵的条件下，B有效地概率为0.85，则发生意外时，两个报警系统至少有一个有效地概率为______________ 答案：0.988
29、设X与Y相互独立且同服从参数为p=1/3的0-1分布，则P{X=Y}=_________ 答案：5/9
30、若事件A与B相互独立，P(A)=0.4，P(A+B)=0.6，则P(B) =_____________ 答案：1/3
一、 计算 1、某种电子元器件的使用寿命X是随即变量，服从指数分布，平均寿命为1000小时.规定使用寿命在500小时以下为废品，产值为0元；使用寿命在500到1000小时之间为次品，产值为10元；使用寿命在1000到1500小时之间为二等品，产值为30元；使用寿命在1500小时以上者为一等品，产值为40元.求该产品的平均产值. 答案：15.65
2、随机向量(X,Y)服从区域D上的均匀分布,其中D由x轴，y轴和x+y=1围成的区域. 设Z=X+Y，求Z的密度函数. 答案：0|1|2
3、设随机变量孑的概率密度函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图48
(1)确定A的值；(2)求分布函数 F(x)；(3)求概率
河南财大成教《概率论与数理统计》专升本课程原题及答案 图49
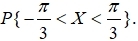
答案：1/2
4、三门高射炮各自独立地射击，它们击中敌机的概率分别为0.6、0.7、0.8. 现三门炮同时各发射一次，求敌机被击中的概率.
答案：0.976
5、随机变量X
答案：如图所示。解析：暂无
6、某年级有400名学生，每天晚上每人去上晚自习的概率为0.8，并且假定每人是否去彼此无关，用中心极限定理求每天晚上至少有300名学生去上晚自习的概率.Φ（(2.5)=0.99379）
答案：0.99379
7、设随机变量X服从区间(0,2)上的均匀分布，求Y=X²的密度函数。 答案：单调递增函数|值域|反函数
8、某公路上跑着的汽车分为载重汽车和非载重汽车，二者数量之比为3:2，已知载重汽车发生故障需中途停下来修理的概率为1%，而非载重汽车中途停修的概率为2%，现有一辆车停下来修理，问它是载重汽车的概率是多少？ 答案：3/7
9、设随机变量X的概率密度函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图50
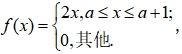
(1)确定a的值；(2)求概率 P{-1<X<0.5}；(3)求分布函数 F(x).
答案：0,0.25
10、10个人中有4个男生，从中任挑两名，若已知两人中有一人是男生，求另一人也是男生的概率. 答案：1/5
11、某超市负责供应某地区10000人的某种商品，若在一段时间内每人需要这种商品的概率为0.2，且各人是否购买彼此无关，问超市应预备这种商品多少件，才能以99.7% 的概率保证不会脱销. (Φ(2.75) = 0.997 ) 答案：2110
12、甲、乙、丙三人在同一时间分别破译某一密码，设他们译出的概率分别为0.6、0.7、0.8，求密码被破译的概率. 答案：0.976
13、已知X~U(0,1)，求Y= 2X+1 的概率密度函数fy(y) 答案：0|1|2|3
14、随机向量(X,Y)服从区域D上的均匀分布，其中D是由x轴，y轴和x+y=1围成的区域.（1）写出(X,Y)的联合密度；（2）求关于X和Y的边缘密度；(3) 判断X与Y是否相互独立. 答案：不互相独立
15、设对于某种少见的疾病的检出率为0.95：即如果某个人患有这种疾病，其检查结果为阳性的概率为0.95；如果该人没有这种疾病，其检查结果为阴性的概率也是0.95。现在假定某一人群中患有这种疾病的概率为0.001，并从这个总体中随机地抽取一个人进行检查，结果为阳性。问这个人患有这种病的概率有多大？ 答案：0.0187
16、随机向量(X,Y)服从区域D上的均匀分布，其中D是由x轴，x=1和y=x围成的区域.（1）写出(X,Y)的联合密度；（2）求关于X和Y的边缘密度；(3) 判断X与Y是否相互独立. 答案：不互相独立
17、树的主人外出，委托邻居浇水. 如果邻居不浇水，树死去的概率为0.8；若浇水，树死去的概率为0.15. 若有0.9的把握确定邻居会记得浇水，（1）求主人回来树还活着的概率；（2）若主人回来树已经死去，求邻居忘记浇水的概率. 答案：16/43
18、某商店负责供应某地区1000人的某种商品，若在一段时间内每人需要一件这种商品的概率为0.6，且各人是否购买彼此无关，问商店应预备这种商品多少件，才能以99.7%的概率保证不会脱销. (Φ(2.75) = 0.997020 ) 答案：643
19、设随机变量x的概率密度函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图51
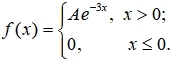
(1)确定A的值；(2)求分布函数F(x)；(3)求概率 P{|X|<1}. 答案：
河南财大成教《概率论与数理统计》专升本课程原题及答案 图52
20、设（X,Y）的联合密度为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图53
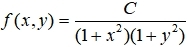
，求:
(1)待定常数 C; (2)P{(X,Y)∈D},其中D={(x,y)|0≤x≤1, 0≤y≤1}.
答案：1/16
21、某电子计算机主机有400个终端，每个终端有80的时间被使用. 若各个终端是否被使用是相互独立的，求至少有300个终端被使用的概率. (Φ(2.5) = 0.99379 )
答案：0.99379
22、设一批混合麦种中一等品、二等品、三等品分别占20%、70%、10%，三个等级的发芽率依次为0.9、0.7、0.3，求：（1）这批麦种的发芽率；（2）若取一粒能发芽，它是二等品的概率.
答案：0.7 23、设随机变量孑的密度函数为
河南财大成教《概率论与数理统计》专升本课程原题及答案 图54
答案： 1/6
24、设随机变量 孑服从区间(1,2)上的均匀分布，求
河南财大成教《概率论与数理统计》专升本课程原题及答案 图55
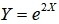
的密度函数。 答案：0|1|2 25、设随机变量
河南财大成教《概率论与数理统计》专升本课程原题及答案 图56
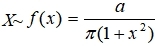
,-∞<x<+∞, 求：(1)常数a的值；(2)分布函数F(x)；(3)P{|X|<1} 答案：1/2 |
