郑州城市学院成教《高等数学》高起专原题及答案 图1
一、单选题
1、设函数
郑州城市学院成教《高等数学》高起专原题及答案 图2
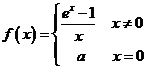在点 x=0 处连续，则a=（ ）。
A、-1
B、0
C、1
D、e
答案：C
2、已知函数
郑州城市学院成教《高等数学》高起专原题及答案 图3
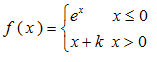在点x=0 处连续 ，则 k=
A、0
B、-1
C、1
D、任意常数
答案：C
3、设y=xarctanx，则y''（0）= （ ）。
A、-2
B、2
C、- 1/2
D、1/2
答案：B
4、与f(x)=
郑州城市学院成教《高等数学》高起专原题及答案 图4
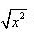等价的函数是___________。
A、x
B、
郑州城市学院成教《高等数学》高起专原题及答案 图5
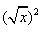
C、
郑州城市学院成教《高等数学》高起专原题及答案 图6
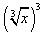
D、|x|
答案：D
5、微分方程y'+2y=4x满足初始条件y|x=0=0的特解为（ ）。
A、y=2x+1+
郑州城市学院成教《高等数学》高起专原题及答案 图7
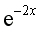
B、y=2x-1+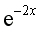
C、y=-2x+1+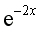
D、y=-2x-1+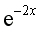
答案：B
6、微分方程（y-2xy-x²）dx+x²dy=0是（ ）
A、线性方程
B、伯努利方程
C、全微分方程
答案：B
7、当x→0时，下列函数中sin²x的高阶无穷小的是___________
A、x²
B、1－cosx
C、3x
D、x³
答案：D
8、曲线y=eˣ在点（0，1）处的切线方程为__________
A、y=x-1
B、y=x+1
C、y=x
D、x≠1
答案：B
9、级数
郑州城市学院成教《高等数学》高起专原题及答案 图8
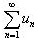的部分和数列{Sₙ}的极限
郑州城市学院成教《高等数学》高起专原题及答案 图9
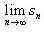存在是级数收敛的（ ）
A、充分条件
B、必要条件
C、充分必要条件
D、无关条件
答案：C
10、函数f(x)=xcos x是（ ）
A、奇函数
B、 偶函数
C、非奇非偶函数
D、既奇又偶函数
答案：A
11、函数
郑州城市学院成教《高等数学》高起专原题及答案 图10
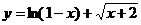的定义域是（ ）。
A、[-2,1]
B、[-2,1)
C、(-2,1]
D、(-2,1)
答案：B
12、设函数f(x)=xsin x-ln x,则f' (π)=
A、π＋1/π
B、π－1/π
C、﹣π＋1/π
C、﹣π－1/π
答案：D
13、设y = x arccos x ,则y''(0)=
A、-1
B、1
C、0
D、-2
答案：C
14、设方程 确定了是的函数，则（ ） e ʸ+xy=e y x y'(0)=
A、1；
B、- 1/e;
C、-1；
D、1/e
答案：B
15、
郑州城市学院成教《高等数学》高起专原题及答案 图11
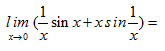
A、0
B、1
C、∞
D、不存在
答案：B
16、设f(x)=eˣ,g(x)=lnx, 则g(f(x))=
A、0
B、1
C、x
D、lnx
答案：C
17、函数f(x)=x²|sinx|的图形
A、关于x轴对称
B、关于y轴对称
C、关于原点对称
D、关于直线y=x对称
答案：B
18、
郑州城市学院成教《高等数学》高起专原题及答案 图12
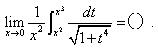
A、3
B、1
C、-1
答案：C
19、
郑州城市学院成教《高等数学》高起专原题及答案 图13
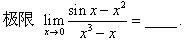
A、1
B、-1
C、∞
答案：B
20、设函数
郑州城市学院成教《高等数学》高起专原题及答案 图14
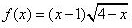，则f(x)在区间______上满足罗尔定义条件
A、(1,4)
B、[1,4]
C、[-2,2]
D、[0,6]
答案：B
二、多选题
21、函数f(x)在区间[a,∞)内二阶可导， 且f'(x)<0，f''(x)<0，则曲线y=f(x)在区间[a,+∞)内
A、曲线单调减少
B、曲线单调增加
C、曲线既不增、也不减
D、曲线图形上凹(凹弧)
E、曲线图形下凹（凸弧)
答案：AE
22、设函数g(x)=xf(x²) ,则 g(x) 是（ ）
A、偶函数
B、奇函数
C、图形关于原点对称的函数
D、图形关于y轴对称的函数
答案：BC
23、函数f(x)在区间[a,+ ∞)内二阶可导， 且 f'(x)<0，f''(x)<0,则曲线y=f(x)在区间[a,+∞)内
A、曲线单调减少
B、曲线单调增加
C、曲线既不增、也不减
D、曲线图形上凹(凹弧)
E、曲线图形下凹（凸弧)
答案：AE
24、函数f(x)在区间[a,+∞)内二阶可导，且f'(x)>0,f''(x)>0，则曲线y=f(x)在区间[a,+∞)内
A、曲线单调减少
B、曲线单调增加
C、曲线既不增、也不减
D、曲线图形上凹(凹弧)
E、曲线图形下凹（凸弧)
答案：BE
25、下列函数中为奇函数的是（ ）。
A、x+sin x
B、x²sin x
C、x²cos x
D、x+cos x
答案：AB
三、问答题
26、证明方程x⁵+x-1=0只有一个正根。
答案：
证明：设f(x)=x⁵+x-1，则f(0)=-1<0，f(1)=1>0，由零点定理知方程 x x⁵+x-1=0在0和1之间有一个（正）根，若方程x⁵+x-1=0有两个正根a,b,a>b>0,则由罗尔定理知存在§:a>§ b>0，使得5§⁴+1=0，但这显然是不可能的, 所以方程x⁵+x-1=0只有一个正根。
|
